1. Graph
· 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조
· 정점 (vertex) : 데이터, 그래프에서 점
· 간선 (edge) : 점과 점을 이어주는 선
· 가중치 그래프 : 가중치(연결의 강도)가 적혀있는 그래프
· 비가중치 그래프 : 가중치가 적혀있지 않은 그래프

2. 알아두어야 할 Graph 용어💡
· 무향 그래프(undirected graph) <-> 단방향 그래프(directed graph)
· 진입차수(in-degree) / 진출차수(out-degree) : 한 정점에서 진입(들어오는 간선)과 진출(나가는 간선)의 개수
· 인접(adjacency) : 두 정점 간에 간선이 직접 이어져 있는 경우 -> 두 정점은 인접한 정점!
· 자기 루프(self roop) : 정점에서 진출하는 간선이 바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다고 표현한다.
· 사이클(cycle) : 한 정점에서 출발해 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다. (순환 느낌?!?)
※참고 : 인접 행렬 & 인접 리스트
· 인접 행렬 : 정점들 간의 인접함을 표시해 주는 행렬 -> 2차원 배열

· 인접 리스트 : 각 정점이 어떤 정점과 인접하는지 리스트의 형태로 볼 수 있는 표현 방식

3. Tree
· 하나의 뿌리로부처 가지가 사방을 뻗은 형태 (일방향 그래프)
· 계층적 자료구조 + 비선형 구조 + 사이클 X
· 루트 (root) : 트리 구조의 시작 데이터 (꼭짓점!!)
· 노드 (node) : 간선으로 연결되는 각각 데이터들 (부모 노드, 자식 노드, 리프 노드)
· 레벨 (level) : 노드와 노드의 간격 (거리)
· 깊이 (depth) : 특정 노드부터 시작해 루트까지의 레벨

4. 트리의 종류
1. 이진 트리 (Binary Tree)
· 자식 노드가 최대 2개인 노드들로 구성된 트리 (왼쪽 자식 , 오른쪽 자식)
· 자료의 삽입, 삭제 방법 -> 정 이진 트리, 완전 이진 트리, 포화 이진 트리
· 정 이진 트리(Full Binary Tree) : 각 노드가 0개 or 2개의 자식 노드를 갖는 트리
· 완전 이진 트리(Complete Binary Tree) : 마지막 레벨을 제외한 모든 노드가 가득 차야 하고, 마지막 레벨의 노드는 왼쪽은 채워져야 하는 트리
· 포화 이진 트리(Perfect Binary Tree) : 정 이진 트리 & 완전 이진 트리, 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리
2. 이진 탐색 트리 (Binary Search Tree)
모든 왼쪽 자식들은 루트나 부모보다 작은 값이고, 모든 오른쪽 자식들은 루트나 부모보다 큰 값인 트리
5. 트리 순회
· 어떠한 특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것
· 순회 순서는 항상 왼쪽부터 오른쪽으로!!
· 루트의 위치 -> 전위 순회, 중위 순회, 후위 순회
· 전위 순회 : 루트 노드부터 시작 -> 왼쪽 자식 노드가 있으면 왼쪽부터!!

· 중위 순회 : 루트를 가운데에 두고 순회!! 제일 왼쪽 끝에 있는 노드부터 시작 -> 루트 거쳐 오른쪽으로 이동
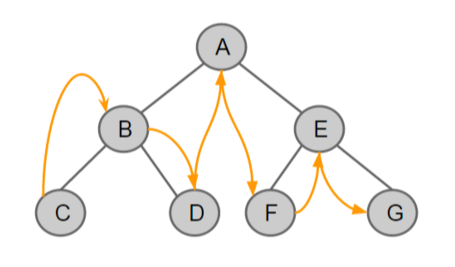
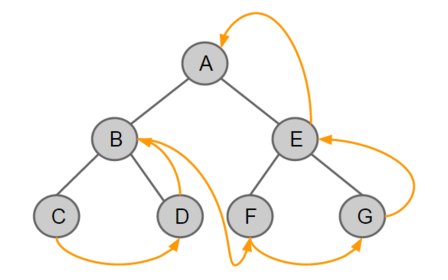
· 후위 순회 : 루트를 제일 마지막으로 순회!! 제일 왼쪽 끝에 있는 노드부터 시작 -> 루트 거치지 X 오른쪽으로 이동
'TIL 👩🏻💻' 카테고리의 다른 글
| TIL : Algorithm (2) (0) | 2021.04.20 |
|---|---|
| TIL : Algorithm (1) (0) | 2021.04.19 |
| TIL : Stack & Queue (0) | 2021.04.14 |
| TIL : Subclass Dance Party (0) | 2021.04.13 |
| TIL : BeesBeesBees (0) | 2021.04.12 |